Let’s visit a couple of fun and extremely counterintuitive problems which sit in the same family. The first appears to be a “paradox,” and illustrates a subtle fallacy. The second is an absolutely astonishing (and legitimate) algorithm for achieving better than 50-50 oods of picking the higher of two unknown envelopes. Plenty of articles have discussed who discovered what ad nauseum so we’ll just dive into the problems.
— The Two Envelope Paradox: Optimizing Expected Return —
First, consider the following scenario. Suppose you are shown two identical envelopes, each containing some amount of money unknown to you. You are told that one contains double the money in the other (but not which is which or what the amounts are) and are instructed to choose one. The one you select is placed in front of you and its contents are revealed. You then are given a second choice: keep it or switch envelopes. You will receive the amount in the envelope you choose. Your goal is to maximize your expected payment.
Our intuition tells us that no information has been provided by opening the envelope. After all, we didn’t know the two values beforehand so learning one of them tells us nothing. The probability of picking the higher envelope should be  regardless of whether we switch or not. But you weren’t asked to improve on the probability, just to maximize your expected payment. Consider the following 3 arguments:
regardless of whether we switch or not. But you weren’t asked to improve on the probability, just to maximize your expected payment. Consider the following 3 arguments:
- Let the amount in the the envelope you initially chose be
 . If it is wrong to switch then the other envelope contains
. If it is wrong to switch then the other envelope contains 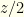 , but if it is right to switch it contains
, but if it is right to switch it contains 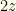 . There are even odds of either, so your expectation if you switch is
. There are even odds of either, so your expectation if you switch is  . This is better than the
. This is better than the  you get by sticking with the initial envelope, so it always is better to switch!
you get by sticking with the initial envelope, so it always is better to switch! - Since we don’t know anything about the numbers involved, opening the first envelope gives us no information — so ignore that value. Call the amount in the other envelope
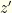 . If it is wrong to switch then the envelope you chose contains
. If it is wrong to switch then the envelope you chose contains 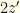 , and if right to switch it contains
, and if right to switch it contains 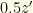 . If you switch, you get
. If you switch, you get 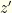 but if you don’t your expectation is
but if you don’t your expectation is  . So it always is better NOT to switch!
. So it always is better NOT to switch! - Call the amounts in the two envelopes
 and
and 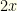 (though you don’t know which envelope contains which). You pick one, but there is equal probability of it being either
(though you don’t know which envelope contains which). You pick one, but there is equal probability of it being either  or
or 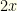 . The expected reward thus is
. The expected reward thus is 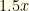 . If you switch, the same holds true for the other envelope. So you still have an expected reward of
. If you switch, the same holds true for the other envelope. So you still have an expected reward of 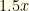 . It doesn’t matter what you do.
. It doesn’t matter what you do.
Obviously, something is wrong with our logic. One thing that is clear is that we’re mixing apples and oranges with these arguments. Let’s be a bit more consistent with our terminology. Let’s call the value that is in the opened envelope  and the values in the two envelopes
and the values in the two envelopes  and
and 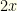 . We don’t know which envelope contains each, though. When we choose the first envelope, we observe a value
. We don’t know which envelope contains each, though. When we choose the first envelope, we observe a value  . This value may be
. This value may be  or
or 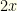 .
.
In the 3rd argument,  . If we switch, then
. If we switch, then 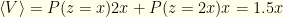 . If we keep the initial envelope then
. If we keep the initial envelope then  . Whether we switch or not, the expected value is
. Whether we switch or not, the expected value is 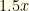 though we do not know what this actually is. It could correspond to
though we do not know what this actually is. It could correspond to 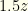 or
or 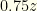 . We must now draw an important distinction. It is correct that
. We must now draw an important distinction. It is correct that  for the known
for the known  and given our definition of
and given our definition of  as the minimum of the two envelopes. However, we cannot claim that
as the minimum of the two envelopes. However, we cannot claim that 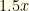 is
is 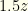 or
or 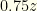 with equal probability! That would be tantanmount to claiming that the envelopes contain the pairs
with equal probability! That would be tantanmount to claiming that the envelopes contain the pairs  or
or 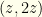 with equal probability. We defined
with equal probability. We defined  to be the minimum value so the first equality holds, but we would need to impose a constraint on the distribution over that minimum value itself in order for the second one to hold. This is a subtle point and we will return to it shortly. Suffice it to say that if we assume such a thing we are led right to the same fallacy the first two arguments are guilty of.
to be the minimum value so the first equality holds, but we would need to impose a constraint on the distribution over that minimum value itself in order for the second one to hold. This is a subtle point and we will return to it shortly. Suffice it to say that if we assume such a thing we are led right to the same fallacy the first two arguments are guilty of.
Obviously, the first two arguments can’t both be correct. Their logic is the same and therefore they must both be wrong. But how? Before describing the problems, let’s consider a slight variant in which you are NOT shown the contents of the first envelope before being asked to switch. It may seem strange that right after you’ve chosen, you are given the option to switch when no additional information has been presented. Well, this really is the same problem. With no apriori knowledge of the distribution over  , it is immaterial whether the first envelope is opened or not before the 2nd choice is made. This gives us a hint as to what is wrong with the first two arguments.
, it is immaterial whether the first envelope is opened or not before the 2nd choice is made. This gives us a hint as to what is wrong with the first two arguments.
There actually are two probability distributions at work here, and we are confounding them. The first is the underlying distribution on ordered pairs or, equivalently, the distribution of the lower element  . Let us call it
. Let us call it 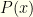 . It determines which two numbers
. It determines which two numbers  we are dealing with. We do not know
we are dealing with. We do not know 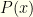 .
.
The second relevant distribution is over how two given numbers (in our case  ) are deposited in the envelopes (or equivalently, how the player orders the envelopes by choosing one first). This distribution unambiguously is 50-50.
) are deposited in the envelopes (or equivalently, how the player orders the envelopes by choosing one first). This distribution unambiguously is 50-50.
The problem arises when we implicitly assume a form for 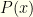 or attempt to infer information about it from the revealed value
or attempt to infer information about it from the revealed value  . Without apriori knowledge of
. Without apriori knowledge of 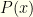 , being shown
, being shown  makes no difference at all. Arguments which rely solely on the even-odds of the second distribution are fine, but arguments which implicitly involve
makes no difference at all. Arguments which rely solely on the even-odds of the second distribution are fine, but arguments which implicitly involve 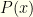 run into trouble.
run into trouble.
The first two arguments make precisely this sort of claim. They implicitly assume that the pairs  or
or 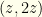 can occur with equal probability. Suppose they couldn’t. For simplicity (and without reducing the generality of the problem), let’s assume that the possible values in the envelopes are constrained to
can occur with equal probability. Suppose they couldn’t. For simplicity (and without reducing the generality of the problem), let’s assume that the possible values in the envelopes are constrained to 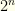 with
with 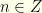 . The envelopes thus contain
. The envelopes thus contain  for some integer
for some integer  (though we don’t know which envelope contains which value). For convenience, let’s work in terms of
(though we don’t know which envelope contains which value). For convenience, let’s work in terms of 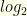 of the values involved (taking care to use
of the values involved (taking care to use 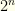 when computing expectations).
when computing expectations).
In these terms, the two envelopes contain 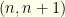 for some
for some 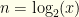 (defined to be the lesser of the two). We open one, and see
(defined to be the lesser of the two). We open one, and see 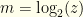 . If it is the upper then the pair is
. If it is the upper then the pair is  , otherwise the pair is
, otherwise the pair is 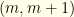 . To claim that these have equal probabilities means that
. To claim that these have equal probabilities means that  and
and 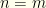 are equally probable. We made this assumption independent of the value of
are equally probable. We made this assumption independent of the value of 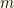 , so it would require that all pairs
, so it would require that all pairs 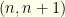 be equally probable.
be equally probable.
So what? Why not just assume a uniform distribution? Well, for one thing, we should be suspicious that we require an assumption about 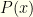 . The 3rd argument requires no such assumption. Even if we were to assume a form for
. The 3rd argument requires no such assumption. Even if we were to assume a form for 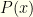 , we can’t assume it is uniform. Not just can’t as in “shouldn’t”, but can’t as in “mathematically impossible.” It is not possible to construct a uniform distribution on
, we can’t assume it is uniform. Not just can’t as in “shouldn’t”, but can’t as in “mathematically impossible.” It is not possible to construct a uniform distribution on  .
.
Suppose we sought to circumvent this issue by constraining ourselves to some finite range ![{[M,N]}](https://s0.wp.com/latex.php?latex=%7B%5BM%2CN%5D%7D&bg=fefeeb&fg=000000&s=0&c=20201002) , which we supposedly know or assume apriori. We certainly can impose a uniform distribution on it. Each pair
, which we supposedly know or assume apriori. We certainly can impose a uniform distribution on it. Each pair 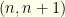 has probability
has probability 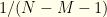 with
with ![{n\in [M,N-1]}](https://s0.wp.com/latex.php?latex=%7Bn%5Cin+%5BM%2CN-1%5D%7D&bg=fefeeb&fg=000000&s=0&c=20201002) . But now we’ve introduced additional information (in the form of
. But now we’ve introduced additional information (in the form of 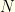 and
and 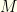 ), and it no longer is surprising that we can do better than even-odds! We always would switch unless the first envelope contained
), and it no longer is surprising that we can do better than even-odds! We always would switch unless the first envelope contained 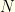 . There is no contradiction between the first two arguments because we have apriori knowledge and are acting on it. We no longer are true to the original game.
. There is no contradiction between the first two arguments because we have apriori knowledge and are acting on it. We no longer are true to the original game.
Rather than dwell on this particular case, let’s solve the more general case of a given 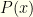 (or in terms of
(or in terms of 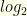 ,
, 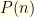 ). For any
). For any  drawn according to
drawn according to 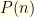 , the envelopes contain
, the envelopes contain 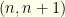 in some order and it is equally likely that
in some order and it is equally likely that  and
and 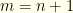 . If we know
. If we know  we can bet accordingly since it contains information. In that case, knowing
we can bet accordingly since it contains information. In that case, knowing 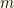 (i.e.
(i.e.  ) helps us. Let’s suppose we don’t know
) helps us. Let’s suppose we don’t know  . Then it still does not matter whether we observe the value
. Then it still does not matter whether we observe the value  , because we don’t the know the underlying distribution!
, because we don’t the know the underlying distribution!
There only are two deterministic strategies: always keep, always switch. Why? Suppose that the drawn value is  (unknown to us) and the observed value is
(unknown to us) and the observed value is 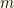 . Note that these don’t require actual knowledge of the
. Note that these don’t require actual knowledge of the 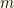 value, just that it has been fixed by the process of opening the envelope. Since we don’t know the underlying distribution, our strategy will be independent of the actual value. Given that the value doesn’t matter, we have nothing to do but always keep or always switch.
value, just that it has been fixed by the process of opening the envelope. Since we don’t know the underlying distribution, our strategy will be independent of the actual value. Given that the value doesn’t matter, we have nothing to do but always keep or always switch.
First consider the expected value with the always-keep strategy:
![\displaystyle \langle V_K \rangle= \sum_{n=-\infty}^\infty P(n) [P(m=n|n) 2^n + P(m=n+1|n) 2^{n+1}]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Clangle+V_K+%5Crangle%3D+%5Csum_%7Bn%3D-%5Cinfty%7D%5E%5Cinfty+P%28n%29+%5BP%28m%3Dn%7Cn%29+2%5En+%2B+P%28m%3Dn%2B1%7Cn%29+2%5E%7Bn%2B1%7D%5D&bg=fefeeb&fg=000000&s=0&c=20201002)
I.e. we sum over all possible ordered pairs 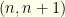 and then allow equal probability
and then allow equal probability 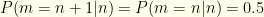 for either of the two envelope orders. So we have
for either of the two envelope orders. So we have 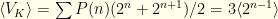 . We immediately see that for this to be defined the probability distribution must drop faster than
. We immediately see that for this to be defined the probability distribution must drop faster than 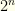 as
as  gets large! We already have a constraint on the possible forms for
gets large! We already have a constraint on the possible forms for  .
.
Next consider the always-switch strategy. It’s easy to see that we get the same result:
![\displaystyle \langle V_S \rangle= \sum_{n=-\infty}^\infty P(n) [P(m=n|n) 2^{n+1} + P(m=n+1|n) 2^{n}]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Clangle+V_S+%5Crangle%3D+%5Csum_%7Bn%3D-%5Cinfty%7D%5E%5Cinfty+P%28n%29+%5BP%28m%3Dn%7Cn%29+2%5E%7Bn%2B1%7D+%2B+P%28m%3Dn%2B1%7Cn%29+2%5E%7Bn%7D%5D&bg=fefeeb&fg=000000&s=0&c=20201002)
and since  we get the same answer.
we get the same answer.
But let’s be extra pedantic, and connect this to the original formulation of the first two arguments. I.e., we should do it in terms of 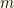 , the observed value.
, the observed value.
![\displaystyle \langle V_S \rangle= \sum_m P(m) [P(n=m|m) 2^{m+1} + P(n=m-1|m) 2^{m-1}]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Clangle+V_S+%5Crangle%3D+%5Csum_m+P%28m%29+%5BP%28n%3Dm%7Cm%29+2%5E%7Bm%2B1%7D+%2B+P%28n%3Dm-1%7Cm%29+2%5E%7Bm-1%7D%5D&bg=fefeeb&fg=000000&s=0&c=20201002)
We observe that  and
and 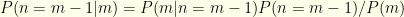 . We know that
. We know that 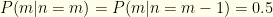 . Plugging these in, we get
. Plugging these in, we get
![\displaystyle \langle V_S \rangle= \sum_m [0.5 P(n=m) 2^{m+1} + 0.5 P(n=m-1) 2^{m-1}]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Clangle+V_S+%5Crangle%3D+%5Csum_m+%5B0.5+P%28n%3Dm%29+2%5E%7Bm%2B1%7D+%2B+0.5+P%28n%3Dm-1%29+2%5E%7Bm-1%7D%5D&bg=fefeeb&fg=000000&s=0&c=20201002)
The first term gives us 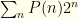 . We can rewrite the index on the 2nd sum to get
. We can rewrite the index on the 2nd sum to get 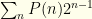 , which gives us
, which gives us 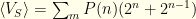 , the exact same expression as before!
, the exact same expression as before!
How does this apply to the ![{[M,N]}](https://s0.wp.com/latex.php?latex=%7B%5BM%2CN%5D%7D&bg=fefeeb&fg=000000&s=0&c=20201002) ranged example we gave before? When we discussed it, we considered the case where the underlying distribution was known. In that and all other cases, a better than even-odds strategy based on such knowledge can be computed. In our actual formulation of the game, we don’t know
ranged example we gave before? When we discussed it, we considered the case where the underlying distribution was known. In that and all other cases, a better than even-odds strategy based on such knowledge can be computed. In our actual formulation of the game, we don’t know 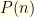 and there’s no reason it couldn’t be uniform on some unknown interval
and there’s no reason it couldn’t be uniform on some unknown interval ![{[M,N]}](https://s0.wp.com/latex.php?latex=%7B%5BM%2CN%5D%7D&bg=fefeeb&fg=000000&s=0&c=20201002) . Suppose it was. It still seems from our earlier discussion as if we’d do better by always switching. We don’t. The average amount thrown away by incorrectly switching when
. Suppose it was. It still seems from our earlier discussion as if we’d do better by always switching. We don’t. The average amount thrown away by incorrectly switching when  exactly offsets the average gain from switching in all other cases. We do no better by switching than by keeping.
exactly offsets the average gain from switching in all other cases. We do no better by switching than by keeping.
We thus see that without knowing the underlying distribution 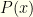 , the switching and keeping strategies have the same expected reward. Of the three arguments we originally proposed, the first 2 were flawed in that they assume a particular, and impossible, underlying distribution for
, the switching and keeping strategies have the same expected reward. Of the three arguments we originally proposed, the first 2 were flawed in that they assume a particular, and impossible, underlying distribution for  .
.
At the beginning of our discussion, we mentioned that our intuition says you cannot do better than 50-50 probability-wise. Let us set aside expected rewards and focus solely on probabilities. We now see how you actually can do better than 50-50, contrary to all intuition!
— Achieving better than 50-50 Odds with Two Envelopes —
Next let’s consider a broader class of two-envelope problems, but purely from the standpoint of probabilities. Now the two envelopes can contain any numbers; one need not be double the other. As before, we may choose an envelope, it is opened, and we are offered the opportunity to keep it or switch. Unlike before, our goal now is to maximize the probability of picking the larger envelope.
Since we are dealing with probabilities rather than expectation values, we don’t care what two numbers the envelopes contain. In fact, they need not be numbers at all — as long as they are distinct and comparable (i.e.  or
or  but not both). To meaningfully analyze the problem we require a slightly stronger assumption, though: specifically that the set from which they be drawn (without repetition) possesses a strict linear ordering. However, it need not even possess any algebraic structure or a metric. Since we are not concerned with expectation values, no such additional structure is necessary.
but not both). To meaningfully analyze the problem we require a slightly stronger assumption, though: specifically that the set from which they be drawn (without repetition) possesses a strict linear ordering. However, it need not even possess any algebraic structure or a metric. Since we are not concerned with expectation values, no such additional structure is necessary.
Our intuition immediately tells us that nothing can be gained by switching. In fact, nothing we do should have any impact on the outcome. After all, the probability of initially picking correctly is  . Switching adds no information and lands us with an identical
. Switching adds no information and lands us with an identical  probability. And that is that, right? It turns out that, contrary to our very strong intuition about the problem, there is in fact a way to improve those odds. To accomplish this, we’ll need to introduce a source of randomness. For convenience of exposition we’ll assume the envelopes contain real numbers, and revisit the degree to which we can generalize the approach later.
probability. And that is that, right? It turns out that, contrary to our very strong intuition about the problem, there is in fact a way to improve those odds. To accomplish this, we’ll need to introduce a source of randomness. For convenience of exposition we’ll assume the envelopes contain real numbers, and revisit the degree to which we can generalize the approach later.
The procedure is as follows:
- Pick any continuous probability distribution
 which has support on all of
which has support on all of  (i.e.
(i.e.  for all real
for all real  ). Most common distributions (normal, beta, exponential, etc) are fine.
). Most common distributions (normal, beta, exponential, etc) are fine. - Choose an envelope and open it. We’ll denote its value
 .
. - Sample some value
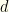 from our distribution
from our distribution  . If
. If  stick with the initial choice, otherwise switch. We’ll refer to
stick with the initial choice, otherwise switch. We’ll refer to  or
or  because the probability that
because the probability that 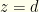 has measure
has measure 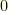 and safely can be ignored.
and safely can be ignored.
At first, second, and 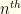 glance, this seems pointless. It feels like all we’ve done is introduce a lot of cruft which will have no effect. We can go stand in a corner flipping a coin, play Baccarat at the local casino, cast the bones, or anything else we want, and none of that can change the probability that we’re equally likely to pick the lower envelope as the higher one initially — and thus equally likely to lose as to gain by switching. With no new information, there can be no improvement. Well, let’s hold that thought and do the calculation anyway. Just for fun.
glance, this seems pointless. It feels like all we’ve done is introduce a lot of cruft which will have no effect. We can go stand in a corner flipping a coin, play Baccarat at the local casino, cast the bones, or anything else we want, and none of that can change the probability that we’re equally likely to pick the lower envelope as the higher one initially — and thus equally likely to lose as to gain by switching. With no new information, there can be no improvement. Well, let’s hold that thought and do the calculation anyway. Just for fun.
First some terminology. We’ll call the value in the opened envelope  , and the value in the other envelope
, and the value in the other envelope 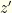 . The decision we must make is whether to keep
. The decision we must make is whether to keep  or switch to the unknown
or switch to the unknown 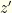 . We’ll denote by
. We’ll denote by  and
and 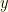 the values in the two envelopes in order. I.e.,
the values in the two envelopes in order. I.e., 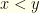 by definition. In terms of
by definition. In terms of  and
and 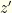 we have
we have 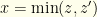 and
and  . We’ll denote our contrived distribution
. We’ll denote our contrived distribution  in the abstract, with pdf
in the abstract, with pdf  and cdf
and cdf 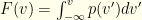 .
.
Let’s examine the problem from a Bayesian perspective. There is a 50-50 chance that 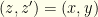 or
or  . So
. So 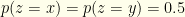 . There are no subtleties lurking here. We’ve assumed nothing about the underlying distribution over
. There are no subtleties lurking here. We’ve assumed nothing about the underlying distribution over 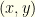 . Whatever
. Whatever 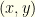 the envelopes contain, we are equally likely to initially pick the one with
the envelopes contain, we are equally likely to initially pick the one with  or the one with
or the one with 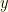 .
.
Once the initial envelope has been opened, and the value  revealed, we sample
revealed, we sample 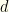 from our selected distribution
from our selected distribution  and clearly have
and clearly have  and
and  and
and 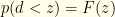 . The latter forms the criterion by which we will keep
. The latter forms the criterion by which we will keep  or switch to
or switch to 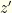 . Please note that in what follows,
. Please note that in what follows, 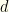 is not a free variable, but rather a mere notational convenience. Something like
is not a free variable, but rather a mere notational convenience. Something like 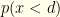 is just notation for “the probability the sampled value is greater than
is just notation for “the probability the sampled value is greater than  .” We can apply Bayes’ law to get (with all probabilities conditional on some unknown choice of
.” We can apply Bayes’ law to get (with all probabilities conditional on some unknown choice of 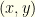 ):
):
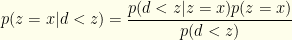
What we really care about is the ratio:

Here, we’ve observed that 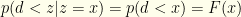 and
and  since by assumption
since by assumption 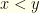 and
and 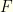 is monotonically increasing (we assumed its support is all of
is monotonically increasing (we assumed its support is all of  ). I.e., if
). I.e., if 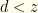 there is a greater probability that
there is a greater probability that  than
than 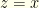 . We shouldn’t switch. A similar argument shows we should switch if
. We shouldn’t switch. A similar argument shows we should switch if  .
.
So what the heck has happened, and where did the new information come from? What happened is that we actually know one piece of information we had not used: that the interval 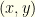 has nonzero probability measure. I.e. there is some “space” between
has nonzero probability measure. I.e. there is some “space” between  and
and 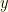 . We don’t know the underlying distribution but we can pretend we do. Our strategy will be worse than if we did know the underlying
. We don’t know the underlying distribution but we can pretend we do. Our strategy will be worse than if we did know the underlying  , of course. We’ll return to this shortly, but first let’s revisit the assumptions which make this work. We don’t need the envelopes to contain real numbers, but we do require the following of the values in the envelopes:
, of course. We’ll return to this shortly, but first let’s revisit the assumptions which make this work. We don’t need the envelopes to contain real numbers, but we do require the following of the values in the envelopes:
- The set of possible values forms a measurable set with a strict linear ordering.
- Between any two elements there is a volume with nonzero probability. Actually, this only is necessary if we require a nonzero improvement for any
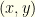 . If we only require an improvement on average we don’t need it. But in that scenario, the host can contrive to use a distribution which neutralizes our strategy and returns us to 50-50 odds.
. If we only require an improvement on average we don’t need it. But in that scenario, the host can contrive to use a distribution which neutralizes our strategy and returns us to 50-50 odds.
What difference does  itself make? We don’t have any way to choose an “optimal” distribution because that would require placing the bulk of probability where we think
itself make? We don’t have any way to choose an “optimal” distribution because that would require placing the bulk of probability where we think  and
and 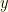 are likely to lie. I.e. we would require prior knowledge. All we can guarantee is that we can improve things by some (perhaps tiny) amount. We’ll compute how much (for a given true underlying distribution) shortly.
are likely to lie. I.e. we would require prior knowledge. All we can guarantee is that we can improve things by some (perhaps tiny) amount. We’ll compute how much (for a given true underlying distribution) shortly.
Let’s assume that 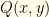 is the true underlying distribution over
is the true underlying distribution over 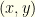 . We won’t delve into what it means to “know”
. We won’t delve into what it means to “know”  since we are handed the envelopes to begin with. Perhaps the game is played many times with values drawn according to
since we are handed the envelopes to begin with. Perhaps the game is played many times with values drawn according to  or maybe it is a one-time affair with
or maybe it is a one-time affair with 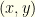 fixed (i.e.
fixed (i.e.  a
a  -distribution). Ultimately, such considerations just would divert us to the standard core philosophical questions of probability theory. Suffice to say that there exists some
-distribution). Ultimately, such considerations just would divert us to the standard core philosophical questions of probability theory. Suffice to say that there exists some 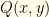 . By definition
. By definition  unless
unless 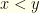 . For convenience, we’ll define a symmetrized version as well:
. For convenience, we’ll define a symmetrized version as well:  . We don’t employ a factor of
. We don’t employ a factor of  since the two terms are nonzero on disjoint domains.
since the two terms are nonzero on disjoint domains.
Given  , what gain do we get from a particular choice of
, what gain do we get from a particular choice of  ?
?
![\displaystyle \begin{array}{rcl} P(win)= \int_{x<y} dx dy Q(x,y)[p(z=x|(x,y))p(x<d) \\ + p(z=y|(x,y))p(d<y)] \end{array}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%5Cbegin%7Barray%7D%7Brcl%7D++P%28win%29%3D+%5Cint_%7Bx%3Cy%7D+dx+dy+Q%28x%2Cy%29%5Bp%28z%3Dx%7C%28x%2Cy%29%29p%28x%3Cd%29+%5C%5C+%2B+p%28z%3Dy%7C%28x%2Cy%29%29p%28d%3Cy%29%5D+%5Cend%7Barray%7D+&bg=fefeeb&fg=000000&s=0&c=20201002)
I.e., the probability we keep  when it is
when it is 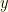 and switch when it is
and switch when it is  . Clearly,
. Clearly,  since those are the immutable 50-50 envelope ordering probabilities. After a little rearrangement, we get:
since those are the immutable 50-50 envelope ordering probabilities. After a little rearrangement, we get:
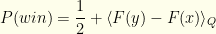
Our gain is the mean value of  over the joint distribution
over the joint distribution 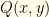 . The more probability
. The more probability  jams between
jams between  and
and 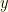 , the more we gain should that
, the more we gain should that 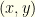 arise. But without knowledge of the underlying joint distribution
arise. But without knowledge of the underlying joint distribution 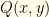 , we have no idea how best to pick
, we have no idea how best to pick  . All we can do is guarantee some improvement.
. All we can do is guarantee some improvement.
How well can we do if we actually know  ? Well, there are two ways to use such information. We could stick to our strategy and try to pick an optimal
? Well, there are two ways to use such information. We could stick to our strategy and try to pick an optimal  , or we could seek to use knowledge of
, or we could seek to use knowledge of  directly. In order to do the former, we need to exercise a little care.
directly. In order to do the former, we need to exercise a little care.  is a two-dimensional distribution while
is a two-dimensional distribution while  is one-dimensional. How would we use
is one-dimensional. How would we use  to pick
to pick  ? Well, this is where we make use of the observed
? Well, this is where we make use of the observed  .
.
In our previous discussion of the  envelope switching fallacy, the value of
envelope switching fallacy, the value of  turned out to be a red-herring. Here it is not. Observing
turned out to be a red-herring. Here it is not. Observing  is essential here, but only for computation of probabilities. As mentioned, we assume no algebraic properties and are computing no expectations. We already know that the observation of
is essential here, but only for computation of probabilities. As mentioned, we assume no algebraic properties and are computing no expectations. We already know that the observation of  is critical, since our algorithm pivots on a comparison between
is critical, since our algorithm pivots on a comparison between  and our randomly sampled value
and our randomly sampled value 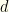 . Considering our ultimate goal (keep or switch), it is clear what we need from
. Considering our ultimate goal (keep or switch), it is clear what we need from  : a conditional probability that
: a conditional probability that  . However, we cannot directly use
. However, we cannot directly use  because we defined
because we defined 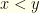 . We want
. We want 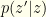 and we don’t know whether
and we don’t know whether  or
or  . Let’s start by computing the probability of
. Let’s start by computing the probability of  (being the observed value) and of
(being the observed value) and of  (being the observed and unobserved values).
(being the observed and unobserved values).
The probability of observing  and the other envelope having
and the other envelope having 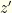 is the probability that the relevant ordered pair was chosen for the two envelopes multiplied by the
is the probability that the relevant ordered pair was chosen for the two envelopes multiplied by the  probability that we initially opened the envelop containing the value corresponding to our observed
probability that we initially opened the envelop containing the value corresponding to our observed  rather than the other one.
rather than the other one.

To get 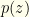 we integrate this.
we integrate this.  . This is a good point to introduce two quantities which will be quite useful going forward.
. This is a good point to introduce two quantities which will be quite useful going forward.
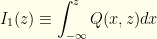
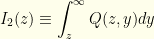
In terms of these,
![\displaystyle p(z)= \frac{1}{2}[I_1(z)+I_2(z)]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+p%28z%29%3D+%5Cfrac%7B1%7D%7B2%7D%5BI_1%28z%29%2BI_2%28z%29%5D&bg=fefeeb&fg=000000&s=0&c=20201002)
There’s nothing special about calling the variables  or
or  in the integrals and it is easy to see (since each only covers half the domain) that we get what we would expect:
in the integrals and it is easy to see (since each only covers half the domain) that we get what we would expect:
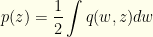
What we want is the distribution  . This gives us:
. This gives us:
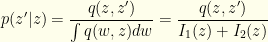
Finally, this gives us the desired quantity 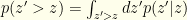 . It is easy to see that:
. It is easy to see that:
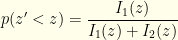

As an example, consider the previous  case — where one envelope holds twice what the other does. We observe
case — where one envelope holds twice what the other does. We observe  , and
, and 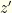 must be either
must be either 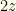 or
or 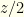 , though we don’t know with what probabilities. If we are given the underlying distribution on
, though we don’t know with what probabilities. If we are given the underlying distribution on  , say
, say  , we can figure that out.
, we can figure that out. 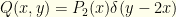 and
and 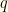 is the symmetrized version.
is the symmetrized version. ![{\int q(w,z)dw= \int dw [Q(w,z)+Q(z,w)]= (P_2(z/2)+P_2(2z))}](https://s0.wp.com/latex.php?latex=%7B%5Cint+q%28w%2Cz%29dw%3D+%5Cint+dw+%5BQ%28w%2Cz%29%2BQ%28z%2Cw%29%5D%3D+%28P_2%28z%2F2%29%2BP_2%282z%29%29%7D&bg=fefeeb&fg=000000&s=0&c=20201002) . So
. So  . This is just what we’d expect — though we’re really dealing with discrete values and are being sloppy (which ends us up with a ratio of infinities from the
. This is just what we’d expect — though we’re really dealing with discrete values and are being sloppy (which ends us up with a ratio of infinities from the  function when computing probability ratios, but we’ll ignore that here). The relevant probability ratio clearly is
function when computing probability ratios, but we’ll ignore that here). The relevant probability ratio clearly is 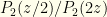 . From a purely probability standpoint, we should switch if
. From a purely probability standpoint, we should switch if 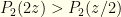 . If we reimpose the algebraic structure and try to compute expectations (as in the previous problem) we would get an expected value of
. If we reimpose the algebraic structure and try to compute expectations (as in the previous problem) we would get an expected value of  from keeping and an expected value of
from keeping and an expected value of ![{z[P_2(z/2)/2 + 2P(2z)]}](https://s0.wp.com/latex.php?latex=%7Bz%5BP_2%28z%2F2%29%2F2+%2B+2P%282z%29%5D%7D&bg=fefeeb&fg=000000&s=0&c=20201002) from switching . Whether this is less than or greater than
from switching . Whether this is less than or greater than  depends on the distribution
depends on the distribution 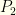 .
.
Returning to our analysis, let’s see how often we are right about switching if we know the actual distribution  and use that knowledge directly. The strategy is obvious. Using our above formulae, we can compute
and use that knowledge directly. The strategy is obvious. Using our above formulae, we can compute 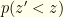 directly. To optimize our probability of winning, we observe
directly. To optimize our probability of winning, we observe  then we switch iff
then we switch iff  . If there is additional algebraic structure and expectations can be defined, then an analogous calculations give whatever switching criterion maximizes the relevant expectation value.
. If there is additional algebraic structure and expectations can be defined, then an analogous calculations give whatever switching criterion maximizes the relevant expectation value.
In terms of probabilities, full knowledge of  is the best we can do. The probability we act correctly is:
is the best we can do. The probability we act correctly is:
![\displaystyle \begin{array}{rcl} P'(win)= \int dz \frac{[\theta(I_1(z)-I_2(z)) I_1(z) + \theta(I_2(z)-I_1(z))I_2(z)]}{I_1(z)+I_2(z)} \\ = \int dz \frac{\max(I_1(z),I_2(z))}{(I_1(z)+I_2(z)} \end{array}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%5Cbegin%7Barray%7D%7Brcl%7D++P%27%28win%29%3D+%5Cint+dz+%5Cfrac%7B%5B%5Ctheta%28I_1%28z%29-I_2%28z%29%29+I_1%28z%29+%2B+%5Ctheta%28I_2%28z%29-I_1%28z%29%29I_2%28z%29%5D%7D%7BI_1%28z%29%2BI_2%28z%29%7D+%5C%5C+%3D+%5Cint+dz+%5Cfrac%7B%5Cmax%28I_1%28z%29%2CI_2%28z%29%29%7D%7B%28I_1%28z%29%2BI_2%28z%29%7D+%5Cend%7Barray%7D+&bg=fefeeb&fg=000000&s=0&c=20201002)

Since 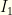 and
and 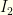 are monotonic (one increasing, the other decreasing), we have a cutoff value
are monotonic (one increasing, the other decreasing), we have a cutoff value 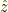 (defined by
(defined by  ) below which we should switch and above which we should not.
) below which we should switch and above which we should not.
How do we do with our invented  instead? We could recast our earlier formula for
instead? We could recast our earlier formula for 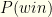 into our current notation, but it’s easier to compute directly. For given
into our current notation, but it’s easier to compute directly. For given  , the actual probability of needing to switch is
, the actual probability of needing to switch is 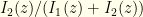 . Based on our algorithm, we will do so with probability
. Based on our algorithm, we will do so with probability 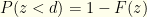 . The probability of not needing to switch is
. The probability of not needing to switch is  and we do so with probability
and we do so with probability 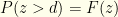 . I.e., our probability of success for given
. I.e., our probability of success for given  is:
is:

For any given  , this is of the form
, this is of the form 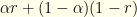 where
where  and
and  . The optimal solutions lie at one end or the other. So it obviously is best to have
. The optimal solutions lie at one end or the other. So it obviously is best to have  when
when 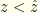 and
and 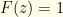 when
when  . This would be discontinuous, but we could come up with a smoothed step function (ex. a logistic function) which is differentiable but arbitrarily sharp. The gist is that we want all the probability in
. This would be discontinuous, but we could come up with a smoothed step function (ex. a logistic function) which is differentiable but arbitrarily sharp. The gist is that we want all the probability in 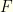 concentrated around
concentrated around 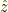 . Unfortunately, we have no idea where
. Unfortunately, we have no idea where 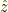 is!
is!
Out of curiosity, what if we pick instead  to be the conditional distribution
to be the conditional distribution 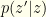 itself once we’ve observed
itself once we’ve observed  ? We’ll necessarily do worse than by direct comparison using
? We’ll necessarily do worse than by direct comparison using  (the max formula above), but how much worse? Well,
(the max formula above), but how much worse? Well,  . Integrating over
. Integrating over  we have
we have 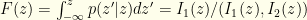 . I.e., We end up with
. I.e., We end up with  as our probability of success. If we had used
as our probability of success. If we had used  for our
for our  instead we would get
instead we would get  instead. Neither is optimal in general.
instead. Neither is optimal in general.
Next, let’s look at the problem from an information theory standpoint. As mentioned, there are two sources of entropy: (1) the choice of the underlying pair 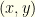 (with
(with 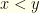 by definition) and (2) the selection
by definition) and (2) the selection 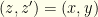 or
or  determined by our initial choice of an envelope. The latter is a fair coin toss with no information and maximum entropy. The information content of the former depends on the (true) underlying distribrution.
determined by our initial choice of an envelope. The latter is a fair coin toss with no information and maximum entropy. The information content of the former depends on the (true) underlying distribrution.
Suppose we have perfect knowledge of the underlying distribution. Then any given  arises with probability
arises with probability ![{p(z)=\frac{1}{2}[I_1(z)+I_2(z)]}](https://s0.wp.com/latex.php?latex=%7Bp%28z%29%3D%5Cfrac%7B1%7D%7B2%7D%5BI_1%28z%29%2BI_2%28z%29%5D%7D&bg=fefeeb&fg=000000&s=0&c=20201002) . Given that
. Given that  , we have a Bernoulli random variable
, we have a Bernoulli random variable 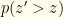 given by
given by 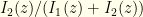 . The entropy of that specific coin toss (i.e. the conditional entropy of the Bernoulli distribution
. The entropy of that specific coin toss (i.e. the conditional entropy of the Bernoulli distribution  ) is
) is
![\displaystyle H(z'>z|z)= \frac{-I_1(z)\ln I(z) - I_2(z)\ln I_2(z) + (I_1(z)+I_2(z))\ln [I_1(z)+I_2(z)]}{I_1(z)+I_2(z)}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+H%28z%27%3Ez%7Cz%29%3D+%5Cfrac%7B-I_1%28z%29%5Cln+I%28z%29+-+I_2%28z%29%5Cln+I_2%28z%29+%2B+%28I_1%28z%29%2BI_2%28z%29%29%5Cln+%5BI_1%28z%29%2BI_2%28z%29%5D%7D%7BI_1%28z%29%2BI_2%28z%29%7D&bg=fefeeb&fg=000000&s=0&c=20201002)
With our contrived distribution  , we are implicitly are operating as if
, we are implicitly are operating as if 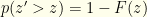 . This yields a conditional entropy:
. This yields a conditional entropy:

There is a natural measure of the information cost of assuming an incorrect distribution. It is the Kullback Liebler Divergence (also known as the relative entropy). While it wouldn’t make sense to compute it between  and
and  (which are, among other things, of different dimension, we certainly can compare the cost for given
(which are, among other things, of different dimension, we certainly can compare the cost for given  of the difference in our Bernoulli random variables for switching — and then integrate over
of the difference in our Bernoulli random variables for switching — and then integrate over  to get an average cost in bits. Let’s denote by
to get an average cost in bits. Let’s denote by  the probability based on the true distribution and keep
the probability based on the true distribution and keep 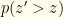 for the contrived one. I.e.
for the contrived one. I.e.  and
and 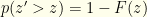 . For given
. For given  , the K-L divergence is:
, the K-L divergence is:
![\displaystyle D(Q || P, z)= \frac{-I_2(z)\ln [(I_1(z)+I_2(z))(1-F(z))/I_2(z)] - I_1(z)\ln [(I_1(z)+I_2(z))F(z)/I_1(z)]}{I_1(z)+I_2(z)}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+D%28Q+%7C%7C+P%2C+z%29%3D+%5Cfrac%7B-I_2%28z%29%5Cln+%5B%28I_1%28z%29%2BI_2%28z%29%29%281-F%28z%29%29%2FI_2%28z%29%5D+-+I_1%28z%29%5Cln+%5B%28I_1%28z%29%2BI_2%28z%29%29F%28z%29%2FI_1%28z%29%5D%7D%7BI_1%28z%29%2BI_2%28z%29%7D&bg=fefeeb&fg=000000&s=0&c=20201002)
Integrating this, we get the mean cost in bits of being wrong.
![\displaystyle \begin{array}{rcl} \langle D(Q || P) \rangle= \frac{1}{2}\int dz [-(I_1(z)+I_2(z))\ln [I_1(z)+I_2(z)] - I_2(z)\ln (1-F(z)) \\ -I_1(z)\ln F(z) + I_1(z)\ln I_1(z) + I_2(z)\ln I_2(z)] \end{array}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%5Cbegin%7Barray%7D%7Brcl%7D++%5Clangle+D%28Q+%7C%7C+P%29+%5Crangle%3D+%5Cfrac%7B1%7D%7B2%7D%5Cint+dz+%5B-%28I_1%28z%29%2BI_2%28z%29%29%5Cln+%5BI_1%28z%29%2BI_2%28z%29%5D+-+I_2%28z%29%5Cln+%281-F%28z%29%29+%5C%5C+-I_1%28z%29%5Cln+F%28z%29+%2B+I_1%28z%29%5Cln+I_1%28z%29+%2B+I_2%28z%29%5Cln+I_2%28z%29%5D+%5Cend%7Barray%7D+&bg=fefeeb&fg=000000&s=0&c=20201002)
The first term is simply 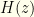 , the entropy of our actual distribution over
, the entropy of our actual distribution over  . In fact, the first term and last 2 terms together we recognize as
. In fact, the first term and last 2 terms together we recognize as 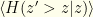 , the mean Bernoulli entropy of the actual distribution. In these terms, we have:
, the mean Bernoulli entropy of the actual distribution. In these terms, we have:
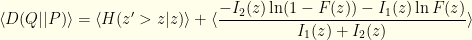
where the expectations are over the unconditional actual distribution 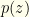 . The 2nd expectation on the right represents the cost of being wrong about
. The 2nd expectation on the right represents the cost of being wrong about  . If it was the optimal distribution with all probability centered near
. If it was the optimal distribution with all probability centered near 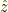 then the term on the right would approach
then the term on the right would approach 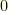 and there would be no entropy cost.
and there would be no entropy cost.
As an aside, this sort of probabilistic strategy should not be confused with the mixed strategies of game theory. In our case, a mixed strategy would be an apriori choice 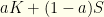 where
where  is the always-keep strategy,
is the always-keep strategy,  is the always-switch strategy, and
is the always-switch strategy, and 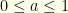 is the probability of employing the always-keep strategy. A player would flip a biased-coin with Bernoulli probability
is the probability of employing the always-keep strategy. A player would flip a biased-coin with Bernoulli probability  and choose one of the two-strategies based on it. That has nothing to do with the measure-theory approach we’re taking here. In particular, a mixes strategy makes no use of the observed value
and choose one of the two-strategies based on it. That has nothing to do with the measure-theory approach we’re taking here. In particular, a mixes strategy makes no use of the observed value  or its relation to the randomly sampled value. Any mixed strategy gives even-odds because the two underlying deterministic strategies both have even-odds.
or its relation to the randomly sampled value. Any mixed strategy gives even-odds because the two underlying deterministic strategies both have even-odds.